Optimizing spiking neural networks¶
Almost all deep learning methods are based on gradient descent, which means that the network being optimized needs to be differentiable. Deep neural networks are usually built using rectified linear or sigmoid neurons, as these are differentiable nonlinearities. However, in biological neural modelling we often want to use spiking neurons, which are not differentiable. So the challenge is how to apply deep learning methods to spiking neural networks.
A method for accomplishing this is presented in Hunsberger and Eliasmith (2015). The idea is to use a differentiable approximation of the spiking neurons during the training process, which can then be swapped for spiking neurons once the optimization is complete. In this example we will use these techniques to develop a network to classify handwritten digits (MNIST) in a spiking convolutional network.
In [1]:
%matplotlib inline
from urllib.request import urlretrieve
import zipfile
import nengo
import nengo_dl
import tensorflow as tf
from tensorflow.contrib.learn.python.learn.datasets import mnist
import numpy as np
import matplotlib.pyplot as plt
First we’ll load the training data, the MNIST digits/labels.
In [2]:
data = mnist.read_data_sets("MNIST_data/", one_hot=True)
for i in range(3):
plt.figure()
plt.imshow(np.reshape(data.train.images[i], (28, 28)))
plt.axis('off')
plt.title(str(np.argmax(data.train.labels[i])));
WARNING:tensorflow:From <ipython-input-2-dcb135e6a60a>:1: read_data_sets (from tensorflow.contrib.learn.python.learn.datasets.mnist) is deprecated and will be removed in a future version.
Instructions for updating:
Please use alternatives such as official/mnist/dataset.py from tensorflow/models.
WARNING:tensorflow:From d:\miniconda3\envs\nengo_dl\lib\site-packages\tensorflow\contrib\learn\python\learn\datasets\mnist.py:260: maybe_download (from tensorflow.contrib.learn.python.learn.datasets.base) is deprecated and will be removed in a future version.
Instructions for updating:
Please write your own downloading logic.
WARNING:tensorflow:From d:\miniconda3\envs\nengo_dl\lib\site-packages\tensorflow\contrib\learn\python\learn\datasets\mnist.py:262: extract_images (from tensorflow.contrib.learn.python.learn.datasets.mnist) is deprecated and will be removed in a future version.
Instructions for updating:
Please use tf.data to implement this functionality.
Extracting MNIST_data/train-images-idx3-ubyte.gz
WARNING:tensorflow:From d:\miniconda3\envs\nengo_dl\lib\site-packages\tensorflow\contrib\learn\python\learn\datasets\mnist.py:267: extract_labels (from tensorflow.contrib.learn.python.learn.datasets.mnist) is deprecated and will be removed in a future version.
Instructions for updating:
Please use tf.data to implement this functionality.
Extracting MNIST_data/train-labels-idx1-ubyte.gz
WARNING:tensorflow:From d:\miniconda3\envs\nengo_dl\lib\site-packages\tensorflow\contrib\learn\python\learn\datasets\mnist.py:110: dense_to_one_hot (from tensorflow.contrib.learn.python.learn.datasets.mnist) is deprecated and will be removed in a future version.
Instructions for updating:
Please use tf.one_hot on tensors.
Extracting MNIST_data/t10k-images-idx3-ubyte.gz
Extracting MNIST_data/t10k-labels-idx1-ubyte.gz
WARNING:tensorflow:From d:\miniconda3\envs\nengo_dl\lib\site-packages\tensorflow\contrib\learn\python\learn\datasets\mnist.py:290: DataSet.__init__ (from tensorflow.contrib.learn.python.learn.datasets.mnist) is deprecated and will be removed in a future version.
Instructions for updating:
Please use alternatives such as official/mnist/dataset.py from tensorflow/models.


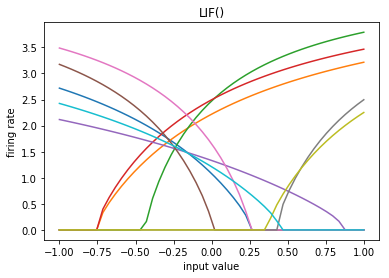
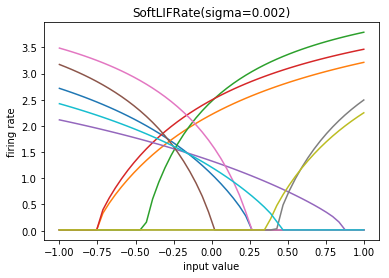
Recall that the plan is to construct the network using a differentiable
approximation of spiking neurons. The spiking neuron model we’ll use is
nengo.LIF, which has the differentiable approximation
nengo_dl.SoftLIFRate. The parameters of nengo_dl.SoftLIFRate are
the same as LIF/LIFRate, with the addition of the sigma parameter
which controls the smoothness of the approximation (the lower the value
of sigma, the closer SoftLIFRate approximates the true
LIF/LIFRate firing curves.
In [3]:
# lif parameters
lif_neurons = nengo.LIF(tau_rc=0.02, tau_ref=0.002, amplitude=0.01)
# softlif parameters (lif parameters + sigma)
softlif_neurons = nengo_dl.SoftLIFRate(tau_rc=0.02, tau_ref=0.002, amplitude=0.01,
sigma=0.002)
# ensemble parameters
ens_params = dict(max_rates=nengo.dists.Choice([100]), intercepts=nengo.dists.Choice([0]))
# plot some example LIF tuning curves
for neuron_type in (lif_neurons, softlif_neurons):
with nengo.Network(seed=0) as net:
ens = nengo.Ensemble(10, 1, neuron_type=neuron_type)
with nengo_dl.Simulator(net) as sim:
plt.figure()
plt.plot(*nengo.utils.ensemble.tuning_curves(ens, sim))
plt.xlabel("input value")
plt.ylabel("firing rate")
plt.title(str(neuron_type))
Building network
Build finished in 0:00:00
Optimization finished in 0:00:00
Construction finished in 0:00:00
Building network
Build finished in 0:00:00
Optimization finished in 0:00:00
Construction finished in 0:00:00
We will use
TensorNodes to
construct the network, as they allow us to easily include features such
as convolutional connections. To make things even easier, we’ll use
nengo_dl.tensor_layer. This is a utility function for constructing
TensorNodes that mimics the layer-based syntax of many deep learning
packages (e.g.
tf.layers).
The full documentation for this function can be found
here.
tensor_layer is used to build a sequence of layers, where each layer
takes the output of the previous layer and applies some transformation
to it. So when we build a tensor_layer we pass it the input to the
layer, the transformation we want to apply (expressed as a function that
accepts a tf.Tensor as input and produces a tf.Tensor as
output), and any arguments to that transformation function.
tensor_layer also has optional transform and synapse
parameters that set those respective values on the Connection from the
previous layer to the one being constructed.
Normally all signals in a Nengo model are (batched) vectors. However,
certain layer functions, such as convolutional layers, may expect a
different shape for their inputs. If the shape_in argument is
specified for a tensor_layer then the inputs to the layer will
automatically be reshaped to the given shape. Note that this shape does
not include the batch dimension on the first axis, as that will be
automatically set by the simulation.
tensor_layer can also be passed a Nengo NeuronType, instead of a
Tensor function. In this case tensor_layer will construct an
Ensemble implementing the given neuron nonlinearity (the rest of the
arguments work the same).
Note that tensor_layer is just a syntactic wrapper for constructing
TensorNodes or Ensembles; anything we build with a
tensor_layer we could instead construct directly using those
underlying components. tensor_layer just simplifies the construction
of this common layer-based pattern.
In [4]:
def build_network(neuron_type):
with nengo.Network() as net:
# we'll make all the nengo objects in the network
# non-trainable. we could train them if we wanted, but they don't
# add any representational power so we can save some computation
# by ignoring them. note that this doesn't affect the internal
# components of tensornodes, which will always be trainable or
# non-trainable depending on the code written in the tensornode.
nengo_dl.configure_settings(trainable=False)
# the input node that will be used to feed in input images
inp = nengo.Node(nengo.processes.PresentInput(data.test.images, 0.1))
# add the first convolutional layer
x = nengo_dl.tensor_layer(
inp, tf.layers.conv2d, shape_in=(28, 28, 1), filters=32,
kernel_size=3)
# apply the neural nonlinearity
x = nengo_dl.tensor_layer(x, neuron_type, **ens_params)
# add another convolutional layer
x = nengo_dl.tensor_layer(
x, tf.layers.conv2d, shape_in=(26, 26, 32),
filters=32, kernel_size=3)
x = nengo_dl.tensor_layer(x, neuron_type, **ens_params)
# add a pooling layer
x = nengo_dl.tensor_layer(
x, tf.layers.average_pooling2d, shape_in=(24, 24, 32),
pool_size=2, strides=2)
# add a dense layer, with neural nonlinearity.
# note that for all-to-all connections like this we can use the
# normal nengo connection transform to implement the weights
# (instead of using a separate tensor_layer). we'll use a
# Glorot uniform distribution to initialize the weights.
x, conn = nengo_dl.tensor_layer(
x, neuron_type, **ens_params, transform=nengo_dl.dists.Glorot(),
shape_in=(128,), return_conn=True)
# we need to set the weights and biases to be trainable
# (since we set the default to be trainable=False)
# note: we used return_conn=True above so that we could access
# the connection object for this reason.
net.config[x].trainable = True
net.config[conn].trainable = True
# add a dropout layer
x = nengo_dl.tensor_layer(x, tf.layers.dropout, rate=0.4)
# the final 10 dimensional class output
x = nengo_dl.tensor_layer(x, tf.layers.dense, units=10)
return net, inp, x
# construct the network
net, inp, out = build_network(softlif_neurons)
with net:
out_p = nengo.Probe(out)
# construct the simulator
minibatch_size = 200
sim = nengo_dl.Simulator(net, minibatch_size=minibatch_size)
Building network
Build finished in 0:00:00
Optimization finished in 0:00:00
Construction finished in 0:00:01
Now we need to train this network to classify MNIST digits. First we load our input images and target labels.
In [5]:
# note that we need to add the time dimension (axis 1), which has length 1
# in this case. we're also going to reduce the number of test images, just to
# speed up this example.
train_inputs = {inp: data.train.images[:, None, :]}
train_targets = {out_p: data.train.labels[:, None, :]}
test_inputs = {inp: data.test.images[:minibatch_size*2, None, :]}
test_targets = {out_p: data.test.labels[:minibatch_size*2, None, :]}
Next we need to define our objective (error) function. Because this is a classification task we’ll use cross entropy, instead of the default mean squared error.
In [6]:
def objective(x, y):
return tf.nn.softmax_cross_entropy_with_logits(logits=x, labels=y)
The last thing we need to specify is the optimizer. For this example we’ll use AdaDelta.
In [7]:
opt = tf.train.AdadeltaOptimizer(learning_rate=1)
In order to quantify the network’s performance we will also define a classification error function (the percentage of test images classified incorrectly). We could use the cross entropy objective, but classification error is easier to interpret.
In [8]:
def classification_error(outputs, targets):
return 100 * tf.reduce_mean(
tf.cast(tf.not_equal(tf.argmax(outputs[:, -1], axis=-1),
tf.argmax(targets[:, -1], axis=-1)),
tf.float32))
Now we are ready to train the network. In order to keep this example
relatively quick we are going to download some pretrained weights.
However, if you’d like to run the training yourself set
do_training=True below.
In [9]:
print("error before training: %.2f%%" % sim.loss(test_inputs, test_targets,
classification_error))
do_training = False
if do_training:
# run training
sim.train(train_inputs, train_targets, opt, objective=objective, n_epochs=5)
# save the parameters to file
sim.save_params("./mnist_params")
else:
# download pretrained weights
urlretrieve(
"https://drive.google.com/uc?export=download&id=0B6DAasV-Fri4WWp0ZFM1XzNfMjA",
"mnist_params.zip")
with zipfile.ZipFile("mnist_params.zip") as f:
f.extractall()
# load parameters
sim.load_params("./mnist_params")
print("error after training: %.2f%%" % sim.loss(test_inputs, test_targets,
classification_error))
sim.close()
error before training: 87.75%
error after training: 1.50%
Now we want to change our network from SoftLIFRate to spiking LIF neurons. We rebuild our network with LIF neurons, and then load the saved parameters.
In [10]:
net, inp, out = build_network(lif_neurons)
with net:
out_p = nengo.Probe(out, synapse=0.1)
sim = nengo_dl.Simulator(net, minibatch_size=minibatch_size, unroll_simulation=10)
sim.load_params("./mnist_params")
Building network
Build finished in 0:00:00
Optimization finished in 0:00:00
Construction finished in 0:00:02
To test our spiking network we need to run it for longer than one timestep, since we can only get an accurate measure of a spiking neuron’s output over time. So we’ll modify our test inputs so that they present the input image for 30 timesteps (0.03 seconds).
In [11]:
n_steps = 30
test_inputs_time = {inp: np.tile(v, (1, n_steps, 1)) for v in test_inputs.values()}
test_targets_time = {out_p: np.tile(v, (1, n_steps, 1)) for v in test_targets.values()}
print("spiking neuron error: %.2f%%" % sim.loss(test_inputs_time, test_targets_time,
classification_error))
spiking neuron error: 3.50%
We can see that the spiking neural network is achieving similar accuracy
as the network we trained with SoftLIFRate neurons. n_steps
could be increased to further improve performance, since we would get a
more accurate measure of each spiking neuron’s output.
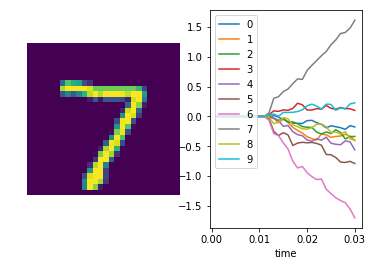
We can also plot some example outputs from the network, to see how it is performing over time.
In [12]:
sim.run_steps(n_steps, input_feeds={inp: test_inputs_time[inp][:minibatch_size]})
for i in range(5):
plt.figure()
plt.subplot(1, 2, 1)
plt.imshow(np.reshape(data.test.images[i], (28, 28)))
plt.axis('off')
plt.subplot(1, 2, 2)
plt.plot(sim.trange(), sim.data[out_p][i])
plt.legend([str(i) for i in range(10)], loc="upper left")
plt.xlabel("time")
Simulation finished in 0:00:01
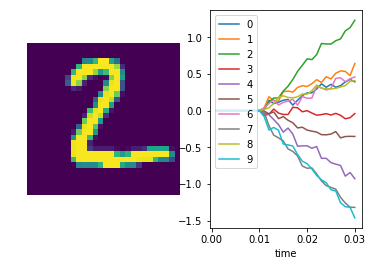
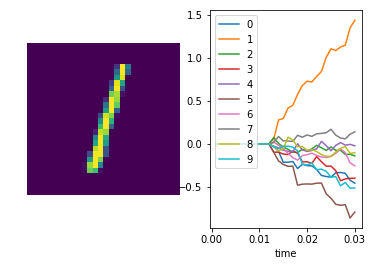
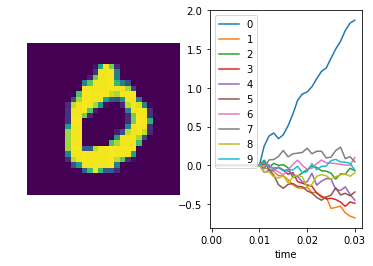
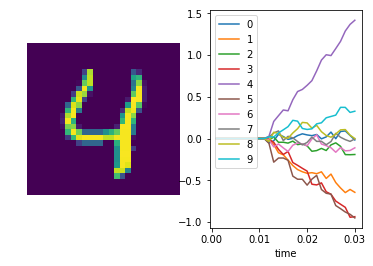
In [13]:
sim.close()