Note

This documentation is for a development version. Click here for the latest stable release (v4.0.0).

Inhibitory gating of ensembles

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

import nengo
from nengo.processes import Piecewise

Step 1: Create the network

Our model consists of two ensembles (called A and B) that receive inputs from a common sine wave signal generator.

Ensemble A is gated using the output of a node, while Ensemble B is gated using the output of a third ensemble (C). This is to demonstrate that ensembles can be gated using either node outputs, or decoded outputs from ensembles.

n_neurons = 30

model = nengo.Network(label="Inhibitory Gating")
with model:
    A = nengo.Ensemble(n_neurons, dimensions=1)
    B = nengo.Ensemble(n_neurons, dimensions=1)
    C = nengo.Ensemble(n_neurons, dimensions=1)

Step 2: Provide input to the model

As described in Step 1, this model requires two inputs.

1. A sine wave signal that is used to drive ensembles A and B

2. An inhibitory control signal used to (directly) gate ensemble A, and (indirectly through ensemble C) gate ensemble B.

with model:
    sin = nengo.Node(np.sin)
    inhib = nengo.Node(Piecewise({0: 0, 2.5: 1, 5: 0, 7.5: 1, 10: 0, 12.5: 1}))

Step 3: Connect the different components of the model

In this model, we need to make the following connections:

1. From sine wave generator to Ensemble A

2. From sine wave generator to Ensemble B

3. From inhibitory control signal to the neurons of Ensemble A (to directly drive the currents of the neurons)

4. From inhibitory control signal to Ensemble C

5. From Ensemble C to the neurons of Ensemble B (this demonstrates that the decoded output of Ensemble C can be used to gate Ensemble B)

with model:
    nengo.Connection(sin, A)
    nengo.Connection(sin, B)
    nengo.Connection(inhib, A.neurons, transform=[[-2.5]] * n_neurons)
    nengo.Connection(inhib, C)
    nengo.Connection(C, B.neurons, transform=[[-2.5]] * n_neurons)

Step 4: Probe outputs

Anything that is probed will collect the data it produces over time, allowing us to analyze and visualize it later. Let’s collect all the data produced.

with model:
    sin_probe = nengo.Probe(sin)
    inhib_probe = nengo.Probe(inhib)
    A_probe = nengo.Probe(A, synapse=0.01)
    B_probe = nengo.Probe(B, synapse=0.01)
    C_probe = nengo.Probe(C, synapse=0.01)

Step 5: Run the model

In order to run the model, we have to create a simulator. Then, we can run that simulator over and over again without affecting the original model.

with nengo.Simulator(model) as sim:
    sim.run(15)

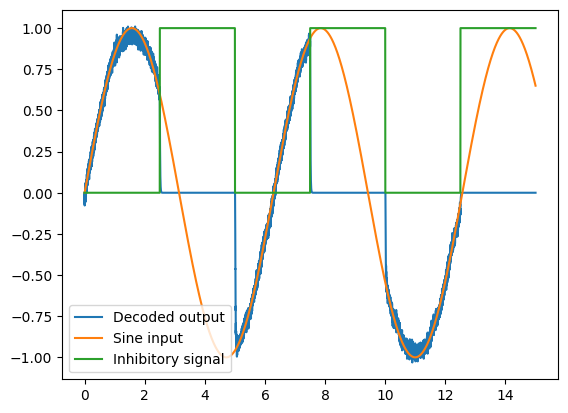
# Plot the decoded output of Ensemble A
plt.figure()
plt.plot(sim.trange(), sim.data[A_probe], label="Decoded output")
plt.plot(sim.trange(), sim.data[sin_probe], label="Sine input")
plt.plot(sim.trange(), sim.data[inhib_probe], label="Inhibitory signal")
plt.legend()

<matplotlib.legend.Legend at 0x7fc1a6d15280>

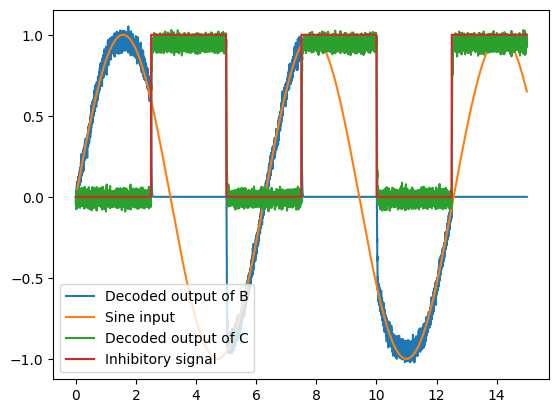
# Plot the decoded output of Ensemble B and C
plt.figure()
plt.plot(sim.trange(), sim.data[B_probe], label="Decoded output of B")
plt.plot(sim.trange(), sim.data[sin_probe], label="Sine input")
plt.plot(sim.trange(), sim.data[C_probe], label="Decoded output of C")
plt.plot(sim.trange(), sim.data[inhib_probe], label="Inhibitory signal")
plt.legend()

<matplotlib.legend.Legend at 0x7fc1a6486970>