Note

This documentation is for a development version. Click here for the latest stable release (v4.0.0).

Controlled oscillator

The controlled oscillator is an oscillator with an extra input that controls the frequency of the oscillation.

To implement a basic oscillator, we would use a neural ensemble of two dimensions that has the following dynamics:

\[\begin{split}\dot{x} = \begin{bmatrix} 0 && - \omega \\ \omega && 0 \end{bmatrix} x\end{split}\]

where the frequency of oscillation is \(\omega \over {2 \pi}\) Hz.

We need the neurons to represent three variables, \(x_0\), \(x_1\), and \(\omega\). According the the dynamics principle of the NEF, in order to implement some particular dynamics, we need to convert this dynamics equation into a feedback function:

\[\begin{split}\begin{align} \dot{x} &= f(x) \\ &\implies f_{feedback}(x) = x + \tau f(x) \end{align}\end{split}\]

where \(\tau\) is the post-synaptic time constant of the feedback connection.

In this case, the feedback function to be computed is

\[\begin{split}\begin{align} f_{feedback}(x) &= x + \tau \begin{bmatrix} 0 && - \omega \\ \omega && 0 \end{bmatrix} x \\ &= \begin{bmatrix} x_0 - \tau \cdot \omega \cdot x_1 \\ x_1 + \tau \cdot \omega \cdot x_0 \end{bmatrix} \end{align}\end{split}\]

Since the neural ensemble represents all three variables but the dynamics only affects the first two (\(x_0\), \(x_1\)), we need the feedback function to not affect that last variable. We do this by adding a zero to the feedback function.

\[\begin{split}f_{feedback}(x) = \begin{bmatrix} x_0 - \tau \cdot \omega \cdot x_1 \\ x_1 + \tau \cdot \omega \cdot x_0 \\ 0 \end{bmatrix}\end{split}\]

We also generally want to keep the ranges of variables represented within an ensemble to be approximately the same. In this case, if \(x_0\) and \(x_1\) are between -1 and 1, \(\omega\) will also be between -1 and 1, giving a frequency range of \(-1 \over {2 \pi}\) to \(1 \over {2 \pi}\). To increase this range, we introduce a scaling factor to \(\omega\) called \(\omega_{max}\).

\[\begin{split}f_{feedback}(x) = \begin{bmatrix} x_0 - \tau \cdot \omega \cdot \omega_{max} \cdot x_1 \\ x_1 + \tau \cdot \omega \cdot \omega_{max} \cdot x_0 \\ 0 \end{bmatrix}\end{split}\]

%matplotlib inline
import matplotlib.pyplot as plt

import nengo
from nengo.processes import Piecewise

Step 1: Create the network

tau = 0.1  # Post-synaptic time constant for feedback
w_max = 10  # Maximum frequency in Hz is w_max/(2*pi)

model = nengo.Network(label="Controlled Oscillator")
with model:
    # The ensemble for the oscillator
    oscillator = nengo.Ensemble(500, dimensions=3, radius=1.7)

    # The feedback connection
    def feedback(x):
        x0, x1, w = x  # These are the three variables stored in the ensemble
        return x0 - w * w_max * tau * x1, x1 + w * w_max * tau * x0, 0

    nengo.Connection(oscillator, oscillator, function=feedback, synapse=tau)

    # The ensemble for controlling the speed of oscillation
    frequency = nengo.Ensemble(100, dimensions=1)

    nengo.Connection(frequency, oscillator[2])

Step 2: Create the input

with model:
    # We need a quick input at the beginning to start the oscillator
    initial = nengo.Node(Piecewise({0: [1, 0, 0], 0.15: [0, 0, 0]}))
    nengo.Connection(initial, oscillator)

    # Vary the speed over time
    input_frequency = nengo.Node(Piecewise({0: 1, 1: 0.5, 2: 0, 3: -0.5, 4: -1}))

    nengo.Connection(input_frequency, frequency)

Step 3: Add Probes

with model:
    # Indicate which values to record
    oscillator_probe = nengo.Probe(oscillator, synapse=0.03)

Step 4: Run the Model

with nengo.Simulator(model) as sim:
    sim.run(5)

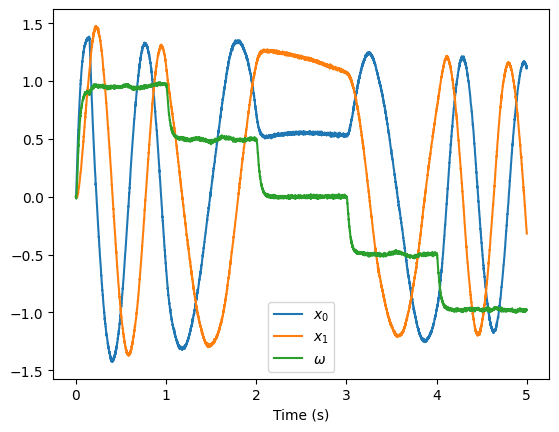
Step 5: Plot the Results

plt.figure()
plt.plot(sim.trange(), sim.data[oscillator_probe])
plt.xlabel("Time (s)")
plt.legend(["$x_0$", "$x_1$", r"$\omega$"])

<matplotlib.legend.Legend at 0x7fee44d21550>