Note
This documentation is for a development version. Click here for the latest stable release (v4.0.0).
Learning to compute a product¶
Unlike the communication channel and the element-wise square, the product is a nonlinear function on multiple inputs. This represents a difficult case for learning rules that aim to generalize a function given many input-output example pairs. However, using the same type of network structure as in the communication channel and square cases, we can learn to compute the product of two dimensions with the nengo.PES learning rule.
The product is a trickier function to learn than the communication channel and the square. We will also try the nengo.RLS learning rule and see how PES and RLS compare in terms of learning the product of two dimensions.
[1]:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import nengo
from nengo.processes import WhiteSignal
Create the model¶
Like previous examples, the network consists of pre, post, and error ensembles. We’ll use two-dimensional white noise input and attempt to learn the product using the actual product to compute the error signal.
[2]:
model = nengo.Network()
with model:
# -- input and pre popluation
inp = nengo.Node(WhiteSignal(60, high=5), size_out=2)
pre = nengo.Ensemble(120, dimensions=2)
nengo.Connection(inp, pre)
# -- post populations
post_pes = nengo.Ensemble(60, dimensions=1)
post_rls = nengo.Ensemble(60, dimensions=1)
# -- reference population, containing the actual product
product = nengo.Ensemble(60, dimensions=1)
nengo.Connection(inp, product, function=lambda x: x[0] * x[1], synapse=None)
# -- error populations
error_pes = nengo.Ensemble(60, dimensions=1)
nengo.Connection(post_pes, error_pes)
nengo.Connection(product, error_pes, transform=-1)
error_rls = nengo.Ensemble(60, dimensions=1)
nengo.Connection(post_rls, error_rls)
nengo.Connection(product, error_rls, transform=-1)
# -- learning connections
conn_pes = nengo.Connection(
pre,
post_pes,
function=lambda x: np.random.random(1),
learning_rule_type=nengo.PES(),
)
nengo.Connection(error_pes, conn_pes.learning_rule)
conn_rls = nengo.Connection(
pre,
post_rls,
function=lambda x: np.random.random(1),
learning_rule_type=nengo.RLS(),
)
nengo.Connection(error_rls, conn_rls.learning_rule)
# -- inhibit errors after 40 seconds
inhib = nengo.Node(lambda t: 2.0 if t > 40.0 else 0.0)
nengo.Connection(inhib, error_pes.neurons, transform=[[-1]] * error_pes.n_neurons)
nengo.Connection(inhib, error_rls.neurons, transform=[[-1]] * error_rls.n_neurons)
# -- probes
product_p = nengo.Probe(product, synapse=0.01)
pre_p = nengo.Probe(pre, synapse=0.01)
post_pes_p = nengo.Probe(post_pes, synapse=0.01)
error_pes_p = nengo.Probe(error_pes, synapse=0.03)
post_rls_p = nengo.Probe(post_rls, synapse=0.01)
error_rls_p = nengo.Probe(error_rls, synapse=0.03)
with nengo.Simulator(model) as sim:
sim.run(60)
[3]:
def plots(start_ix=None, end_ix=None):
sl = slice(start_ix, end_ix)
t = sim.trange()[sl]
plt.figure(figsize=(14, 12))
plt.suptitle("")
plt.subplot(4, 1, 1)
plt.plot(t, sim.data[pre_p][sl], c="b")
plt.legend(("Pre decoding",), loc="best")
plt.subplot(4, 1, 2)
plt.plot(t, sim.data[product_p][sl], c="k", label="Actual product")
plt.plot(t, sim.data[post_pes_p][sl], c="r", label="Post decoding (PES)")
plt.legend(loc="best")
plt.subplot(4, 1, 3)
plt.plot(t, sim.data[product_p][sl], c="k", label="Actual product")
plt.plot(t, sim.data[post_rls_p][sl], c="r", label="Post decoding (RLS)")
plt.legend(loc="best")
plt.subplot(4, 1, 4)
plt.plot(t, sim.data[error_pes_p][sl], c="b", label="Error (PES)")
plt.plot(t, sim.data[error_rls_p][sl], c="r", label="Error (RLS)")
plt.legend(loc="best")
plt.ylim(-1, 1)
plots()
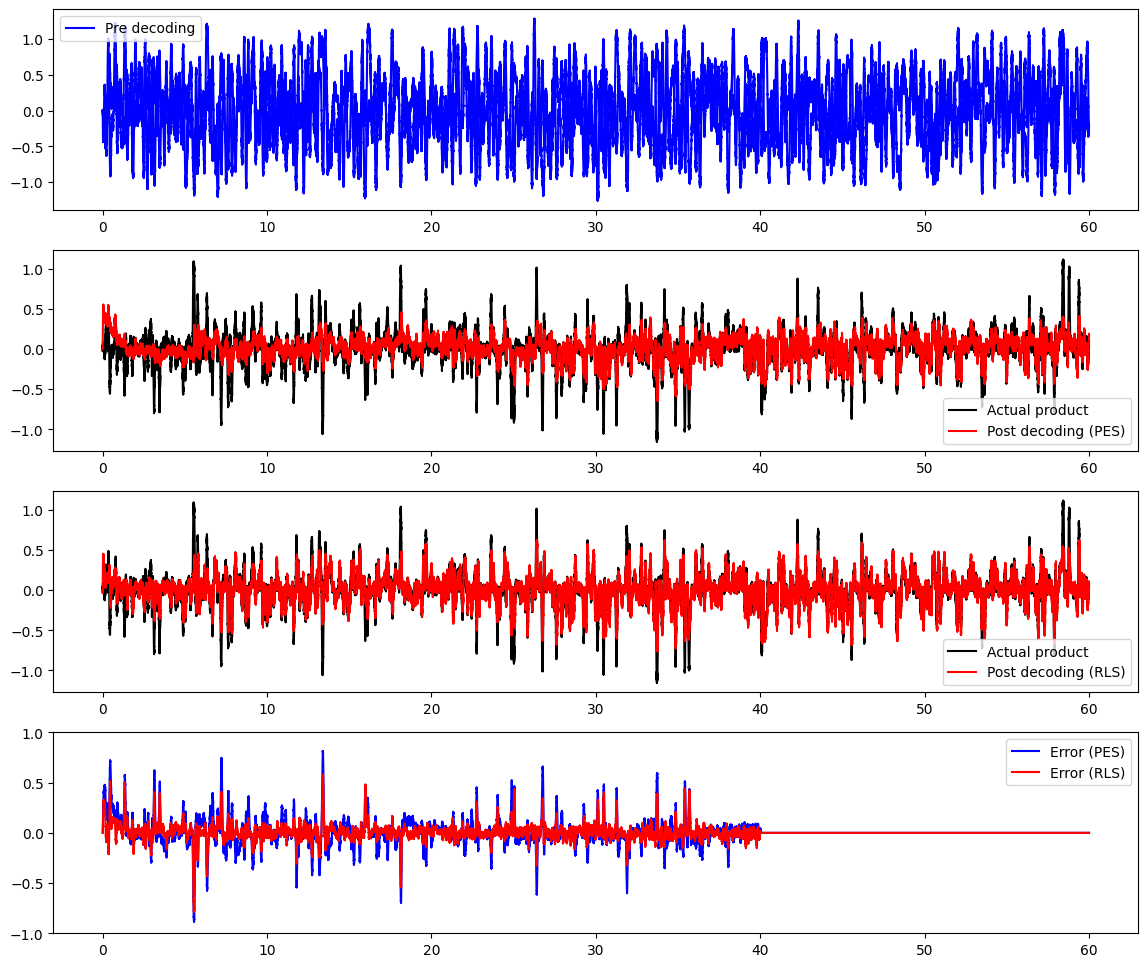
Examine the initial output¶
Let’s zoom in on the network at the beginning:
[4]:
plots(end_ix=2000)
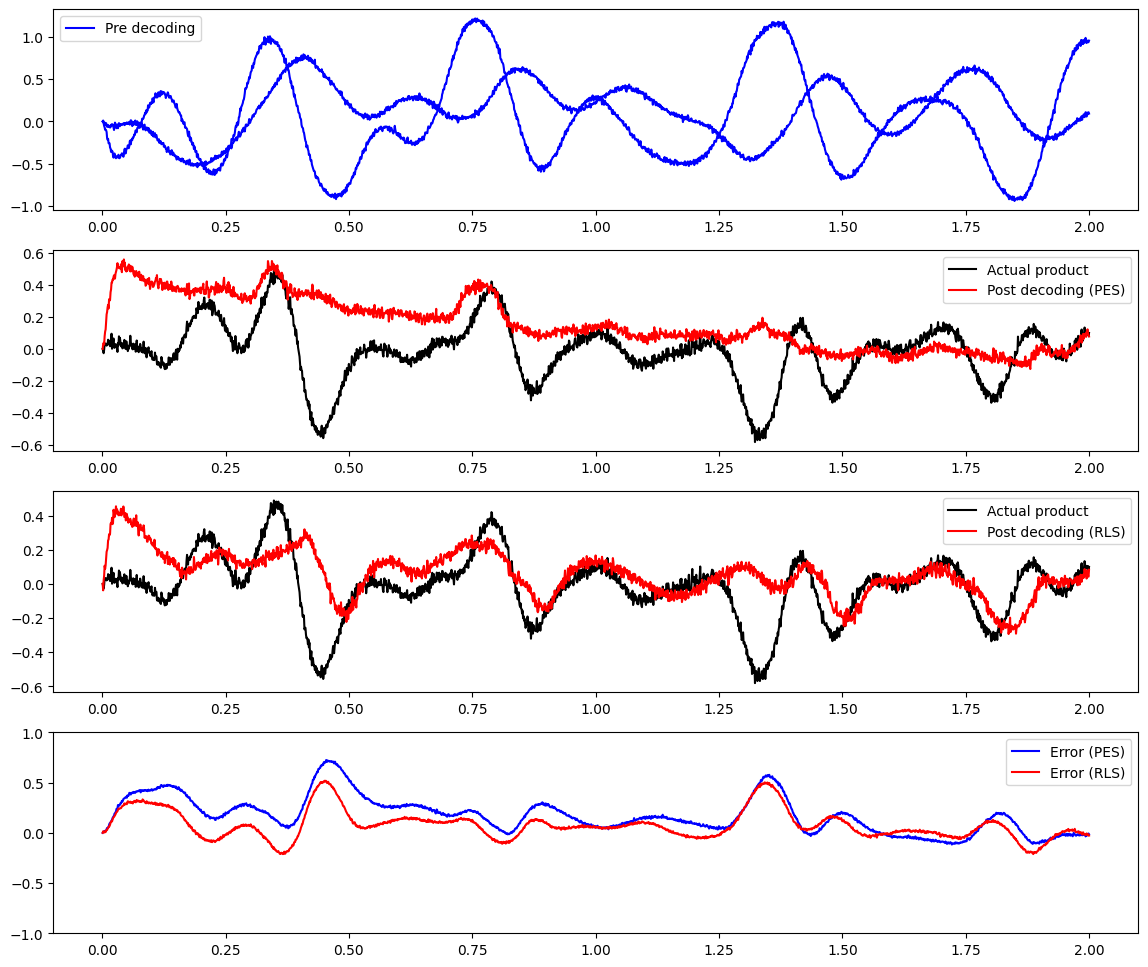
The above plot shows that when the network is initialized, it is not able to compute the product. The error is quite large.
Examine the final output¶
After the network has run for a while, and learning has occurred, the output is quite different:
[5]:
plots(start_ix=38000, end_ix=42000)
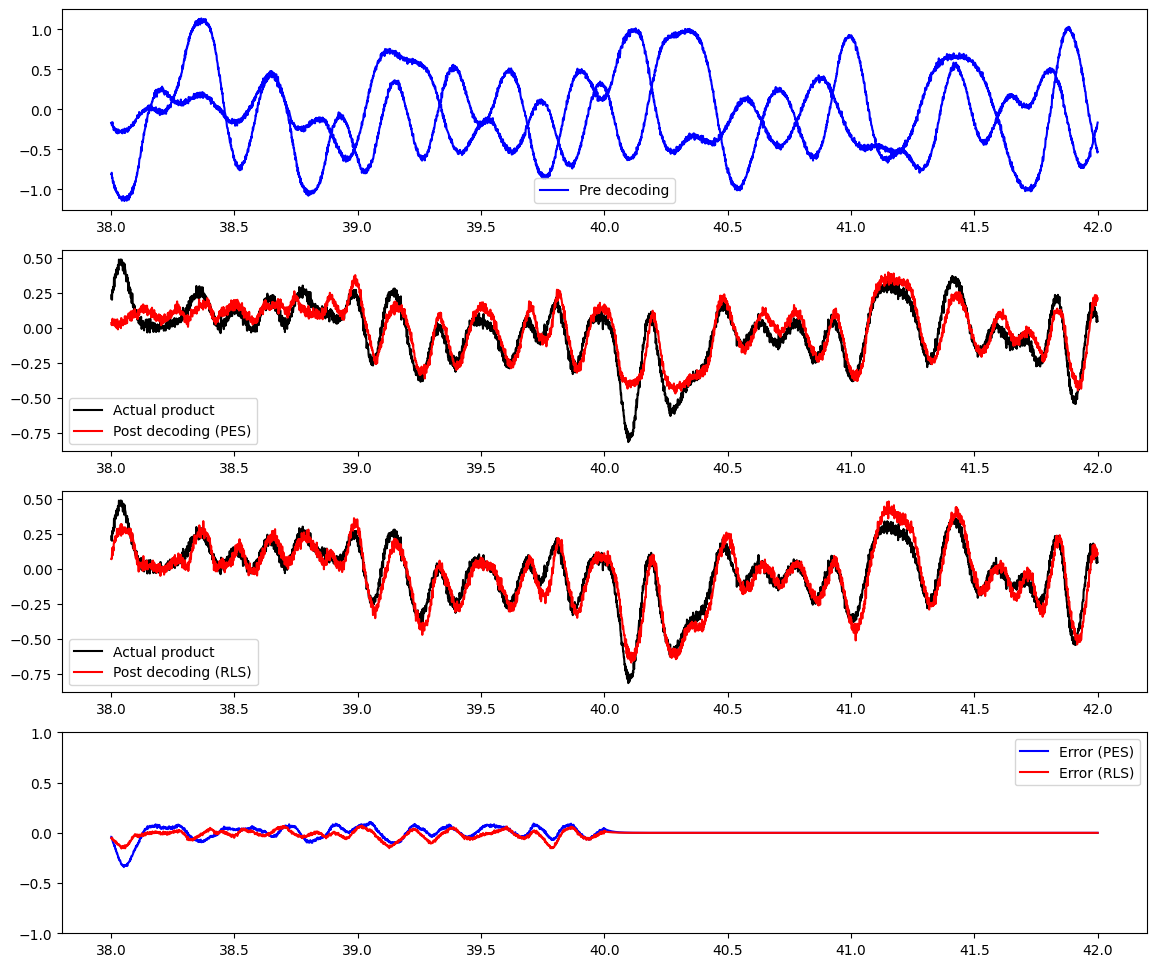
You can see that it has learned a decent approximation of the product, but it’s not perfect – typically, it’s not as good as the offline optimization. The reason for this is that we’ve given it white noise input, which has a mean of 0; since this happens in both dimensions, we’ll see a lot of examples of inputs and outputs near 0. In other words, we’ve oversampled a certain part of the vector space, and overlearned decoders that do well in that part of the space. If we want to do better in other parts of the space, we would need to construct an input signal that evenly samples the space.